统计学让搜索速度起飞
学习资料:
怎么了¶
如果现在有一大批文档,比如你正在看的 莫烦Python, 而你看到一半,发现里面有一些知识点,你并不清楚, 而你又不知道怎么样能快速定位到这个知识点的解释。那么当今摆在你面前的有两个解决方案,一个是使用搜索框,直接搜索这个知识点的关键词, 或者在 莫烦Python 中的导航栏一级级通过分类点击、跳转,最终找到你想要的知识点。
习惯了搜索引擎的我们都偏向于直接搜索,那么我就告诉你一种搜索引擎中常用的技术方法,Term Frequency - Inverse Document Frequency (TF-IDF). 如果用一句话来概括什么是TF-IDF的话,我想我会说: 它使用词语的重要程度与独特性来代表每篇文章,然后通过对比搜索词与代表的相似性,给你提供最相似的文章列表。
另外,TF-IDF并不是一种神经网络或者深度学习,而是一种基于统计学的方法。但它有不可动摇的地位,最主要的原因是搜索中,文档量是巨大的, 而深度学习单个处理每篇文档太慢了,在追求搜索速度时,我们不得不依赖于快速的传统方法。
什么是TF-IDF¶
如果直接解释 TF (词频) IDF (逆文本频率指数),对于从来没接触过这些说法的人,肯定是感觉是云里雾里的。那么请抛开对于这个词的定义 (因为定义你可以百度 / Google找到), 我们直接用通俗的语言来解释。
想象你是新手房产中介,摆在面前的有100个楼盘的文档资料,当客户来咨询楼盘的时候,你必须快速定位到某一篇文档,你会怎么做?我们当然会想要使用某种方法将其归类,什么方法合适呢? 你会不会去找每篇文档中的关键词?那些在某篇文档中出现频率很高的词,比如每篇文档中基本都会有谈论租房
或新房
或二手房
这样的字眼,这些高频的字眼其实就代表着这篇文章的属性, 我们大概也能通过这些字眼判断这是不是客户关心的问题。
但是还有一个问题,很多语气词,没有代表意义的词在一篇文档中同样频率很高,比如我
,中介
,楼盘
,和
这种词,几乎每篇文档中都会存在,而且提及很多次。 它们很明显,虽然词频高,但是不具有区分力,用上面的方法,这些词也会被误认为很重要。所以学者很聪明,他们知道光看局部信息(某篇文档中的词频TF)会带来统计偏差, 它们就引入了一个全局参数(IDF),来判断这个词在所有文档中,是不是垃圾信息。很明显,我
,中介
,和
这种词在全量文档中就是这样的垃圾信息, 而租房
或新房
或二手房
是在全局下有区分力的词。所以如果我们把局部(TF)和全局(IDF)的信息都整合起来一起看的时候,我们就能快速定位到具体的文档啦。
TF-IDF 的数学表达形式¶
其实它就是一个庞大的矩阵,用词语的数字向量来代表一篇文档,当比较文档时,就是在比较这些向量的相似性。比如下面有三篇文档,每篇文档中都不断重复着莫烦
,Python
,最棒
这三个词。 通过对每个词计算TF-IDF后,我们可以用这这些TF-IDF值代表这三篇文档,也就是说,每篇文档就是一个三维向量。
| 莫烦 | Python | 最棒 | |
|---|---|---|---|
| Doc1 | 3 | 12 | 2 |
| Doc2 | 20 | 13 | 6 |
| Doc3 | 22 | 0 | 8 |
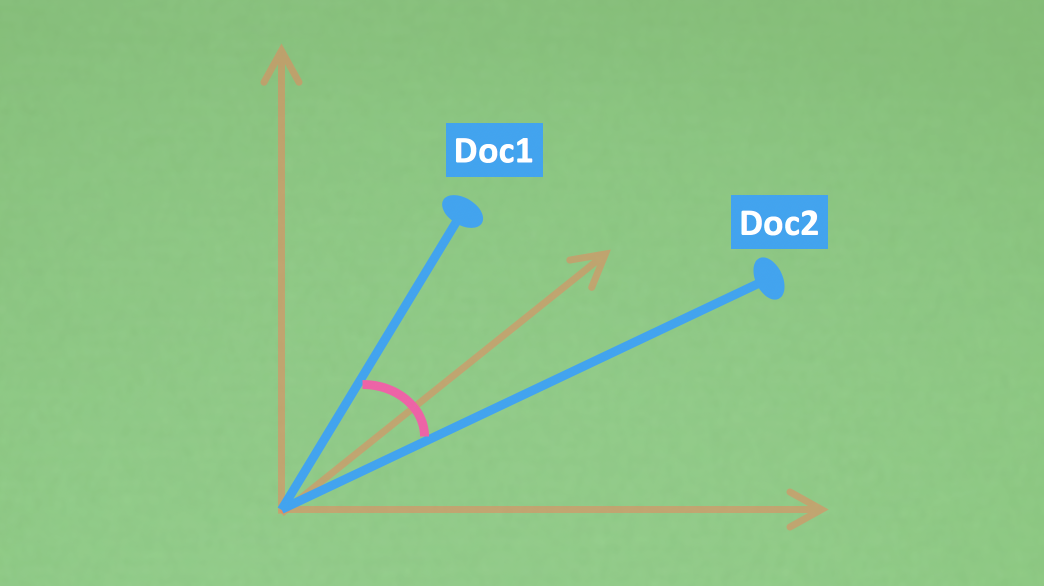
如果把向量展示在图上,就会有类似下面图案的样子,加上一个计算向量相似度的方式,比如cosine距离,我们就能判段哪些文档在这个三维空间上比较相似了。 图中两个蓝色向量离得越近,就代表他们越像。
秀代码¶
说白了,最简单的一个搜索引擎,就是计算好所有的文档向量,然后每次来一个搜索问题,就将这个问题转换成同样的向量,找到那个和问题向量最相近的文档。 这就是很多搜索引擎的本质了。下面我们尝试用Python+Numpy来实现这个过程。如果你习惯直接看所有源码,那么源码在这里。
首先假设我们所有的文档被列在下面,一共15篇,实际中的文档一般都很长,为了举例方便,我就随便写了些段句代替:
将文档的单词转换成ID形式,这样便于后续通过ID进行统计。
首先我们需要构建每一篇文档的代表
,也就是它的TF-IDF向量表示,在计算TF-IDF时,我们会拆开来计算,因为其实IDF的值是可以复用的,当我们计算过一个庞大数据库中的IDF后, 可以把带有这个数据库数据分布的IDF拿到其他地方使用,有点像机器学习当中的与训练模型的意思。举个例子,如果有专门在金融类数据或科技类数据上训练过的NLP的预训练模型, 那么当我们想在科技类文档中使用的当然就是科技类的预训练模型,把金融类的预训练模型放在科技类上使用肯定会存在数据分布上的偏差。同理,IDF预计算表也是这样一个意思。
词w 的IDF本质计算 IDF=log(所有文档数/所有文档中 词w 数), 当然还有很多种变异的计算方式。代码如下:
因为IDF的计算有很多中方法,这里我提供了3种可以选择。一个文档中的词,如果IDF值约小,就说明它越没有意义,在其他文档中出现频率也很高。 最后出来的IDF表是一个所有词语的重要程度表,shape=[n_vocab, 1]. 接下来我们再来计算每篇文档中的TF值。
词w 在 文档d 的TF本质计算 TF=文档d 中 词w 总数
TF 是用所有词组成的每篇文档向量表示,shape=[n_vocab, n_doc], 通过TF-IDF的乘积,就能得到每篇文档的TF-IDF向量表示了。
最终计算出来的TF-IDF实际是一个词语和文章的矩阵,代表着用词语向量表示的文章。
接着,有了这些向量表示,当我们进行搜索时,只需要将搜索的问题向量化,把搜索向量在文档向量上进行距离计算,就能算出来哪些文档更贴近搜索向量了。 我们尝试搜索 I get a coffee cup, 并返回15篇文档当中最像这句搜索的前3篇文档。 (为了突出重点,我简化了docs_score() 的代码, 全部代码在 这可见)
括展思维¶
除了搜索匹配之外,TF-IDF还能干些什么有意思的事情呢?说白了,TF-IDF就是一张将词语重要程度转换成向量的文档展示方式,那么在这些向量中, 必定会有主导型元素,而这些元素其实就是这篇文档中很重要的关键词了。bingo~你发现了,我们居然能给这些文档挑选关键词~下面的功能就是给前三篇文档挑两个关键词。
另外,如果IDF是所有文档的全局信息,那么带有不同属性的文档集群可能拥有不同性质的IDF分布。 比如在混合了金融领域的文档和普通文档的数据量中, 这会是个大而全的IDF,任意一个金融的词都可能对金融类搜索很重要, 因为它可以将金融文档和其他类型的文档有效区分开。但是如果我数据库中只有金融的文档, 想要更精准的搜索,这个大而全的IDF就不适合了,那么我需要一个带有金融属性的IDF表来优化对金融子领域的搜索。 这也是IDF比较重要的应用方式之一。
总结¶
有了TF-IDF在手,我们实际上就有了一个文档的数字化表达形式,通过对这种表达形式稍加利用,就能做出搜索,关键词提取这样有用的功能。 下节内容我将带你了解更加简便的TF-IDF使用方式,以及更多括展应用。